).
Sam Loyds classic Square to Cross disection puzzle is an elegant puzzle where a number of additional shapes can be formed beyond the cross and the square. The puzzle was produced by making rods which have the cross section of the pieces. The rods where then cross-cut into 1cm thick pieces. Overall that yieled somewhere between 80 and 100 puzzles. About half of them were then put into wooden boxes with plexiglass lids, the rest were put into origamy boxes (see picture on the right). Actually producing the boxes was much more work than producing the puzzles!
The puzzles had an acompanying leaflet with the problems and solutions
(pdf file of leaflet: ).
An interactive version of solving the problem of fitting all the pieces into the square
can be played by pressing the button on the left.
In 2006 we decided to hand out puzzles for Halloween instead of candy. We made a Halloween themed version of this puzzle as a simple to make handout.
Haloween Problem 1: Make a square pumpkin patch using only the green pieces.
Haloween Problem 2: Make a (larger) square pumpkin patch using all the pieces (aka plant the pumkin in the patch).
In 2009 Karin needed handouts for people to remember what all is needed to become a distinguished toastmasters club. We made a version of Sam Loyd's Square to Cross puzzle in a CD case and produced 20 for the handouts.
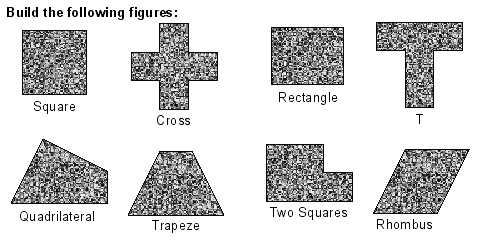
The origin of this dissection is a bit of a mystery. Don Lemon showed such a dissection in his 1890 book “The Illustrated Book of Puzzles”, London: Saxon. However, it is believed that Sam Loyd invented this puzzle as it was published as an advertising puzzle for Scourene in 1887 by the Simonds Soap Company of New York city - Jerry Slocum, “Puzzle Cards”, 1996, color reproduction of eight advertising puzzles.